Calculus of One Variable: Area Under the Curve and The Definite Integral

Recap

Let us make some "mathematical experiments" and make inference with the data that we have gathered. But first, let us review ourselves with integration. What is Integration?

Integration or Antidifferentiation is where we get the antiderivative of a function by using the reverse of differentiation. To better understand this, suppose we have a function:

F(x) = 3x³ + 2x² – 5x + 1

then the derivative of F(x), which is F'(x) is:

F’(x) = 3◦x^3-1 + 2◦2◦x^2-1 – 5◦1x^1-1 +0

F’(x) = 3x² + 4x¹ – 5x⁰ 

F’(x) = 3x² + 4x – 5

Using differentiation, we obtained the derivative of F(x), that is F'(x), suppose we say that let A'(x) = F'(x), then how should we antidifferentiate it?

A’(x) = 3x² + 4x¹ – 5

let the resulting function be A(x), then:

all multiplications become divisions and all subtractions become additions. So, we have:

A(x) = x³ + 2x² – 5x + C

where C there is an indefinite constant, also known as the constant of integration

We call A(x) as the integral of A'(x), where we have seen that antidifferentiation is the reverse of differentiation.

Therefore, by Leibniz notation, we could tell that:

where the symbol ⌠ is what we call the integral sign, F'(x) the integrand, F(x) the integral, and C the constant of integration.

So, that's it! We are done with the review. Are you ready with the "experiment"? :)

Area

We wished to find the area between a function under it and the x-axis. How should we have it done?

Let us have first the simplest graph, the horizontal line graph represented by f(x)=m, where m is a constant. So, we would let the area between f and the x-axis defined over the interval [0,x]. That forms a rectangle that sits on the interval on x-axis. So:

The vertical line from the number x on the x-axis to the line graph above it has length m while the horizontal line from the origin to the number x on the x-axis has length x. Do you know why? Since we let the area of the rectangle formed, that green area over the interval [0,x], the horizontal lines will obtain the length x since those lines extend x-number of units from the point of origin. The vertical lines also extend m-number of units.

Since we have the length x and width m, we could compute for the area of the rectangle, or the area between the function f and the x-axis. That is given by:

A = Length x Width

A = mx

If we would let A be an area function A(x), and x be any number: that is, the x would not be a definite value anymore and will now vary, then:

A(x) = mx

This function A(x) is a graph of a line with y-intercept 0 and slope m. It's graph now would be something like this:

Now, let us consider the linear function f(x) = mx and the area between it and the x-axis over the interval [0,x]. This forms a triangle figure.

Likewise, the length of the vertical line is mx (since the line extends from the number x on the x-axis to the line graph with the function output mx)and the length of the base is x. Thus,:

A = one half of base times height

A = (1/2)(mx)(x)

A = (1/2) mx²

Now, we let x vary and have the area function:

A(x) = (1/2) mx²

^{The graph of A(x) somehow looks like this:}

Now for the conjecture:

Let us tally first our data:

What have you observed? Isn't it that the area function A(x) is the Integral of the function f(x)? Now let us investigate the theorem:

Theorem:

"Let f be a positive continuous function on an interval [a,b] and let A(x) be the area of the region between the graph of f and the x-axis on the interval [a'x]. Then A(x) is a differentable function of x and

A'(x) = f(x)"

Proof:

Let that green area be A(x), so that its derivative is as follows:

Remember that A(x+h) is the total area (red and green) and A(x) is the green area. Now considering A(x+h) - A(x) gives us the area of the small portion (red). This small portion has the area approximately of that rectangle with base h (that is, the horizontal line at the bottom of the red area) and height f(x) (that is, the vertical line from the value x + h to the horizontal line of value f(x).Thus:

A(x+h) - A(x) = Area of the Small Portion

A(x+h) - A(x) = Area of a Rectangle (base x height)

A(x+h) - A(x) ≈ f(x)◦h

So that:

Now it is proven that A'(x) = f(x). Going back to the theorem, we could then say that the area function of any continuous function is the antiderivative, or integral of that function. We also conclude that the area function and any antiderivative of the function differs by a constant. Now, let us have some sample exercises:

Exercises 1: Find the area under the graph of y = x²  on the interval [-3,2].

First, we must define C. To do that, we accept the fact that there is NO area above the x-value -3, or A(-3) = 0, so that if:

f(x) = x²

A(x) = X³/3 + C

so:

A(-3) = (-3)³/3 + C

0 = -27/3 + C

C = 9

Now, we have the value of C. This would set the area from x=-3. The next thing is to use the same area function with the new constant value to x=2. Thus:

A(x) = X³/3 + 9

A(2) = (2)³/3 + 9

A(2) = 35/3

* The Area between the graph of f and the x-axis on the interval [-3,2] is 35/3.

The Definite Integral

We have the theorem about antidifferentiation. It states that:

"If two functions F and G have the same derivative on an interval, then

F(x) = G(x) + C"

This shows that if F and G have the same derivative on an interval, say f, then the two must differ by a constant. What if we defined the interval as [a,b]? If they differ by a constant, then:

If: F(x) = G(x) + C, then

F(b) - F(a) = [G(b) + C] - [G(a) + C]

= G(b) - G(a) + C - C

F(b) - F(a) = G(b) - G(a)

Therefore we could say that the difference F(b) - F(a) is equal to all antiderivatives of f. This difference is defined as the definite integral of f from a to b.Thus:

Where F is any antiderivative of f.

Let us make use of them!

Example 2: Integrate 

Using the antiderivative X³/3 + x, we have:

=(4 )³/3 + 4 - [(3)³/3 + 3]

=40/3

Please note that on a given interval [a,b], since a<b, then b, the larger one is on the top of the notation.

This becomes more exciting if you discover something other than that. For once, let us look at a given situation:

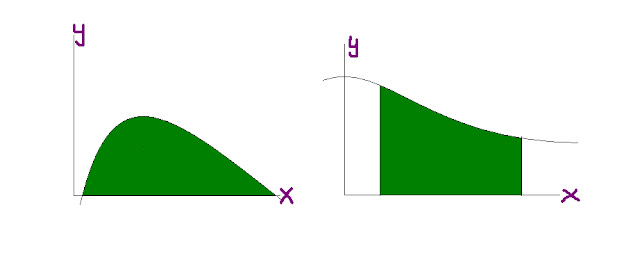
Let A(x) be the area of the region on the interval [0,x], then A'(x) = f(x), this means that A(x) is an antiderivative of f. Is that so? Then we could say that the difference A(b) - A(a) is the same for all antiderivatives of f.Thus, we could say in terms of definite integral that:

Now, isn't it that A(b) - A(a) is the area over [0,b] minus the area over [0,a], which is the area over [a,b]?

By definition, therefore, we say that if we:

"Let f be a positive continuous function over closed interval [a,b]. The area under the graph of f on the interval [a,b] is

"

How about doing similar exercise?

Exercise 3: Find the area under the graph of y = x²  on the interval [-3,2].

Now, we use the definite integral, so that:

* So the area under the graph on the interval [-3,2] is 35/3 square units.

EFY, Krizelle Rubi B. Deza

Works Cited:

Bittinger, Marvin L. and Morrel, Bernard B. Applied Calculus.Canada: Addison-Wesley Publishing Company, Inc., 1984.